本文共 3905 字,大约阅读时间需要 13 分钟。
回归函数可以选择的表示很多。但是根据奥卡姆剃刀原则,应该选择简单而又可行的回归函数。显然,如果可行,,线性函数是最简单的回归函数。当回归函数$F$采用线性模型表示时 ,我们称该类模型为线性回归(linear regression)。线性模型简单,易于建模,由于$\omega$直观的表达了个属性再预测中的重要性,因此线性模型有很好的可解释性(comprehensibility)。
对于样例$(\boldsymbol{x},y)$,当我们希望线性模型的预测值逼近真实标记y时,就得到了线性回归模型,我们把线性回归模型简写为:$$ y=\boldsymbol{\omega}^{T}\boldsymbol{x}+b $$
.
其中系数$omega,b∈R$称为回归系数(regression coefficient)。求回归系数通常有两种方法,除了上文提到的基于最小二乘的normal equation,还有就是通过梯度下降来求解,关于梯度下降可以去看小威精的这篇从梯度下降说起。这里不多说了(有空把线代再重学一学之后再来补充(/▽\)),网上搜了一个梯度下降和Normal equation的区别总结: 线性回归模型,我们知道实际上是通过多个自变量对自变量进行曲线拟合。我们希望找到一条可以较好拟合的曲线,那我们如何判断一条曲线的拟合程度的好坏?上文在推到出来的结果
线性回归模型,我们知道实际上是通过多个自变量对自变量进行曲线拟合。我们希望找到一条可以较好拟合的曲线,那我们如何判断一条曲线的拟合程度的好坏?上文在推到出来的结果 $$ J(\theta)=\sum_{i=1}^{m}(y^{(i)}-\theta^{T}x^{(i)})^{2} $$
中,我们知道的是最小二乘法(预测值和真实值得误差的平方和),原理是正态分布。
对数线性回归(log-linear regression)
$$ lny=\boldsymbol{\omega}^T\boldsymbol{x}+b. (1) $$
它实际上是试图让$e^{\boldsymbol{\omega}^T\boldsymbol{x}+b}$逼近$y$,(1)式在形式上仍然式线性回归,但实质上是在求取输入空间到输出空间的非线性函数映射。如下图,这里的对数函数起到了将线性回归模型的预测值与真实标记联系起来的作用。
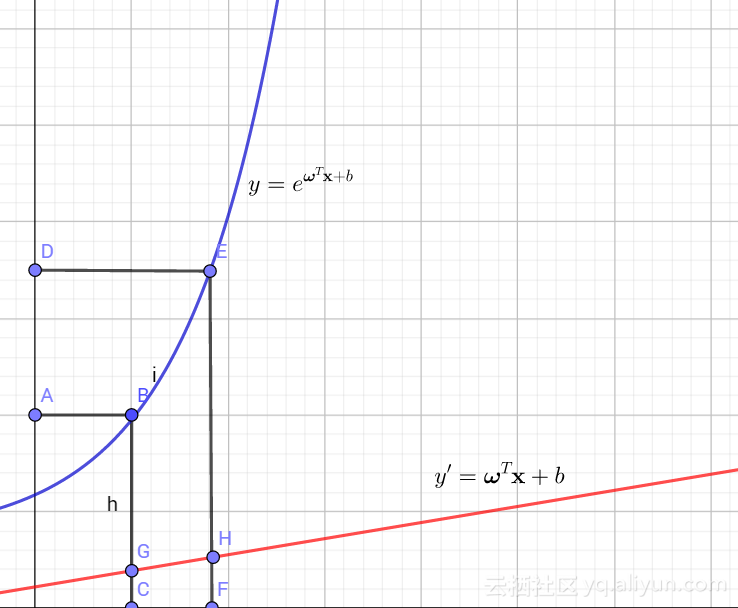 更一般的,考虑单调可微函数$g(⋅)$,令
更一般的,考虑单调可微函数$g(⋅)$,令 $$ y=g^{-1}(\boldsymbol{\omega}^T\boldsymbol{x}+b) $$
这样得到的模型称为“广义线性模型”(generalized linear model),其中函数$g(⋅)$称为“联系函数”(link function).显然,对数线性回归是广义线性模型在$g(⋅)=ln(⋅)$时的特例。
对数几率回归
如果要用线性模型解决分类任务,只需在广义线性模型中找一个单调可微函数将分类任务的真实标记$y$与线性模型的预测值联系起来。
举个例子,对于对于二分类任务,其输出标记$y∈{0,1}$,将线性回归模型预测的连续值来转换为0和1。采用“单位阶跃函数”(nuit-step function)$$ y=\left\{\begin{matrix}0,&z<0\\0.5,& z=0\\ 1,& z>0\end{matrix}\right. $$
即预测值大于零就判断为正例,小于零则判断为反例,预测值为临界值零则可任意判别,如图:
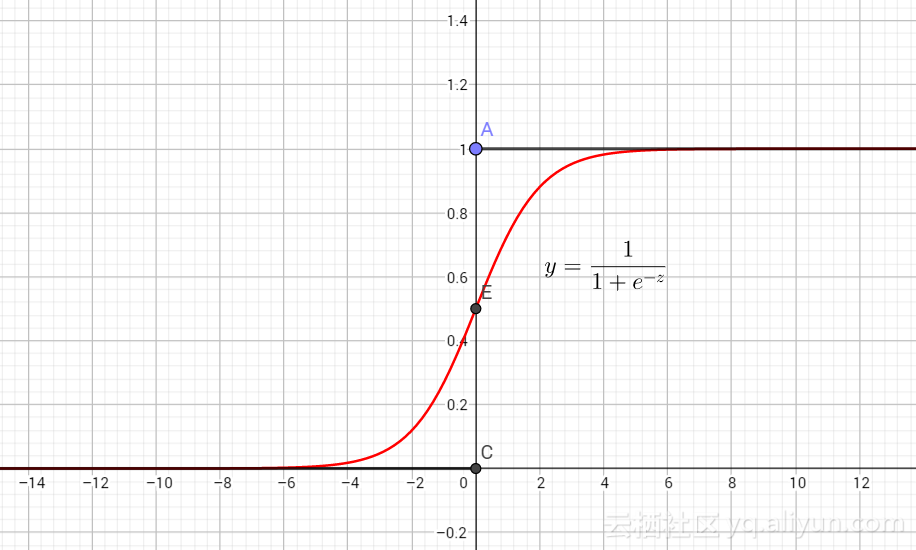 单位阶跃函数不连续,于是需要一个“替代函数”(surrogate function):
单位阶跃函数不连续,于是需要一个“替代函数”(surrogate function): $$ y=\frac{1}{1+e^{-z}} $$
对数几率函数是一种“Sigmoid函数”,它将z值转化为一个接近0或1的y值,并且其输出值在$z=0$附近变化很陡,将对数几率函数作为$g^{-1}(⋅)$带入(2)式,得:
$$ y=\frac{1}{1+e^{-(\boldsymbol{\omega}^T\boldsymbol{x}+b)}} (3) $$
整理得:
$$ ln\frac{y}{1-y}=\boldsymbol{\omega}^T\boldsymbol{x}+b (4) $$
若将$y$视为样本$x$作为正例的可能性,则$1-y$是其反例的可能性,两者的比值
$$ \frac{y}{1-y} $$
称为“几率”(odds),反应了$\boldsymbol{x}$作为正例的相对可能性。对几率取对数则可得到“对数几率”(log odds,亦称logit)
$$ ln\frac{y}{1-y} $$
由此可以看出,式(3)是在用线性回归模型的预测结果去逼近真实标记的“对数几率”(结合式(4)),因此,其对应的模型称为“对数几率回归”(logistics regression,亦称logit regression)。
对于“对数几率回归”,有几点需要注意:名字虽然式回归,但实际确实一种分类学习方法优点:直接对分类可能性进行建模,无需事先假设数据分布,这样就避免了假设分布不准确所带来的问题不仅是预测出“类别”,而是可以得到近似概率预测,这对许多需要利用概率辅助决策的任务很有 用对数函数是任意阶可导的凸函数,现有的许多数值优化算法都可直接用于求取最优解下面来看看如何确定式(3)中的$\boldsymbol{\omega}$和$b$。若将式(3)中的$y$视为类后验概率估计$p(y=1|\boldsymbol{x}$,则式(4)可重写为$$ ln\frac{p(y=1|\boldsymbol{x})}{p(y=0|\boldsymbol{x})}=\boldsymbol{x}^T\boldsymbol{x}+b $$
可以得到:
$$ p(y=1|\boldsymbol{x})=\frac{e^{\boldsymbol{\omega}^T\boldsymbol{x}+b}}{1+e^{\boldsymbol{\omega}^T\boldsymbol{x}+b}} (7) $$
$$ p(y=0|\boldsymbol{x})=\frac{1}{1+e^{\boldsymbol{\omega}^T\boldsymbol{x}+b}} (8) $$
于是,我们可以通过“极大似然法”(maximum likelihood method)来估计$\omega$和$b$。
注:极大似然估计可以看这篇博客[最大似然估计总结(转载)](给定数据集$\left \{ (\boldsymbol{x}_{i},y_{i}) \right \}_{i=1}^{m}$,对率回归模型:似然函数:$L(\boldsymbol{\omega},b)=\prod_{i=1}^{m}p(y_{i}|\boldsymbol{x}_{i};\boldsymbol{\omega},b)$.对数似然:$ι (boldsymbol{omega},b)=sum_{i=1}^{m}lnp(y_{i}|boldsymbol{x}_{i};boldsymbol{omega},b) (5)$“对数似然”最大化,即零每个样本属于其真实标记的概率越大越好。为了方便讨论,令$\boldsymbol{\beta}=(\boldsymbol{\omega};b),\hat{\boldsymbol{x}}=(\boldsymbol{x};1)$则$\boldsymbol{\omega}^{T}\boldsymbol{x}+b$可简写为$\boldsymbol{\beta}^T\hat{\boldsymbol{x}}$。再令$p_{1}(\hat{\boldsymbol{x}};\boldsymbol{\beta})=p(y=1|\hat{\boldsymbol{x}};\boldsymbol{\beta}) $,$p_{0}(\hat{\boldsymbol{x}};\boldsymbol{\beta})=p(y=0|\hat{\boldsymbol{x}};\boldsymbol{\beta})=1-p_{1}(\hat{\boldsymbol{x}};\boldsymbol{\beta})$,则式(5)中的似然项可重写为$$ p(y_{i}|\boldsymbol{x}_{i};\boldsymbol{\omega},b)=y_{i}p_{1}(\hat{\boldsymbol{x}};\boldsymbol{\beta}) $$
$$ +(1-y_{i})p_{0}(\hat{\boldsymbol{x}};\boldsymbol{\beta}) (6) $$
将式(6)带入式(5)中,并根据式(7)(8)可知,最大化式(5)等价于最小化(取相反数):
$$ \imath (\boldsymbol{\beta})=\sum_{i=1}^{m}(-y_{i}\boldsymbol{\beta}^{T}\hat{\boldsymbol{x}}_{i}+ln(1+e^{\boldsymbol{\beta}^T\hat{\boldsymbol{x}}_{i}})) $$
上式是关于$\boldsymbol{\beta}$的高阶可导连续凸函数,根据凸优化理论,经典的数值优化算法如梯度下降(gradient descent method)、牛顿法(Newton method)等都可求得其最优解。
线性回归也终于告一段落了,后文就是周志华《机器学习》的原文,写的实在式太精彩了,现在的水平没法补充什么,就厚颜无耻的“记”下来吧o(▽)q